1. Konsep Peluang (Probabilitas)

Peluang adalah dasar dari semua jenis taruhan. Misalnya, dalam lempar koin:

• Peluang muncul kepala = 50% (0.5)

• Peluang muncul ekor = 50% (0.5)

Dalam dunia taruhan, penyelenggara tidak selalu membayar sesuai dengan peluang yang sebenarnya — di sinilah mereka mendapatkan keuntungan.

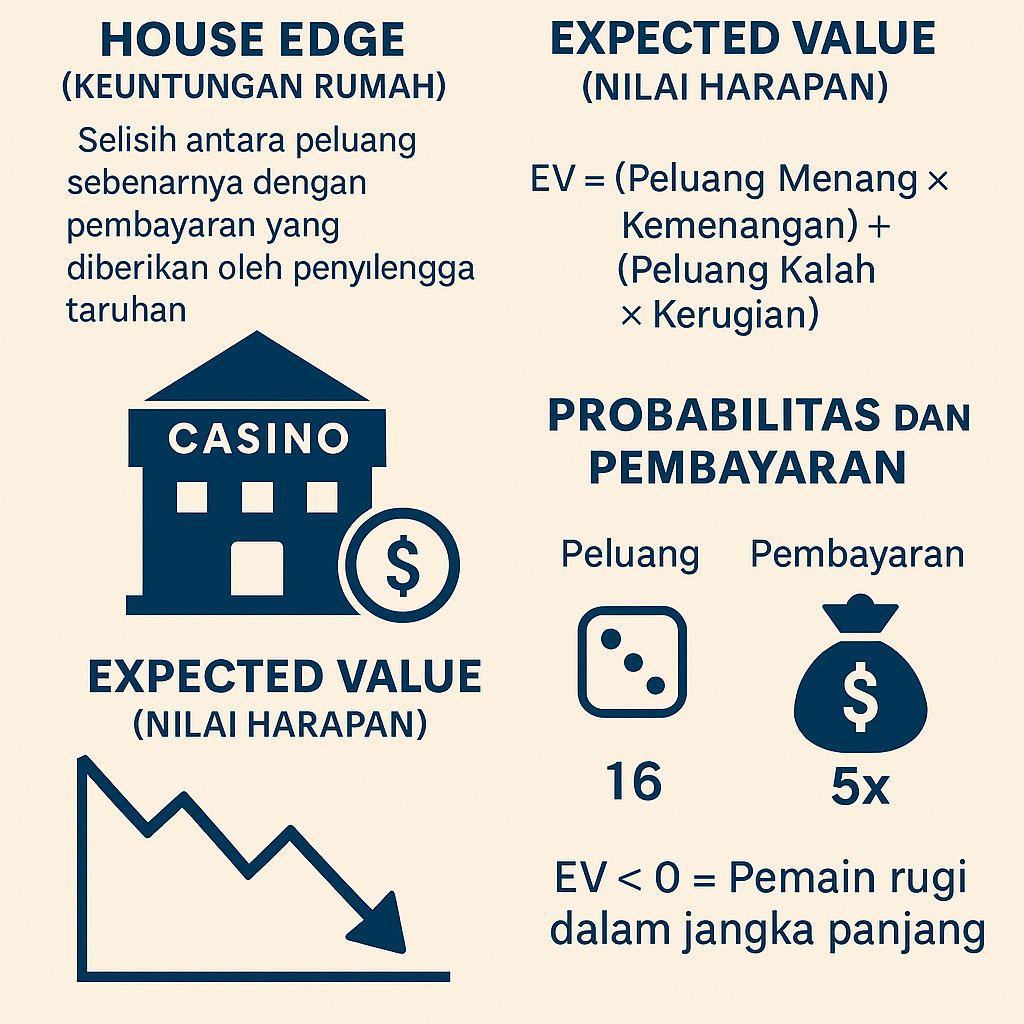
2. House Edge (Keuntungan Rumah)

Ini adalah selisih antara peluang sebenarnya dan pembayaran yang diberikan oleh penyelenggara taruhan.

Contoh: Taruhan pada dadu 6 sisi

• Peluang menang jika menebak satu angka: 1/6 ≈ 16.67%

• Jika rumah membayar 6x lipat, maka pemain “adil” — tapi biasanya hanya dibayar 5x saja.

• Keuntungan rumah (house edge) bisa dihitung:

Expected Value=(16×5)+(56×−1)=0.833−0.833=−0.167\text{Expected Value} = \left(\frac{1}{6} \times 5\right) + \left(\frac{5}{6} \times -1\right) = 0.833 – 0.833 = -0.167Expected Value=(61​×5)+(65​×−1)=0.833−0.833=−0.167

Artinya, setiap kali taruhan 1 unit, rata-rata pemain kehilangan 0.167 unit.

3. Expected Value (Nilai Harapan)

Ini adalah rata-rata hasil dari taruhan yang diulang berkali-kali.

$$EV=(PeluangMenang\times Kemenangan)+(PeluangKalah\times Kerugian)$$

Jika EV bernilai negatif, maka secara statistik pemain akan kalah dalam jangka panjang.

4. Variance & Volatilitas

• Variance: Mengukur seberapa jauh hasil individu dari rata-rata (EV).

• Taruhan dengan pembayaran tinggi (seperti lotre atau jackpot) punya variance tinggi, artinya hasilnya sangat tidak konsisten.

• Taruhan seperti roulette merah/hitam lebih rendah variansinya.

5. Ilusi Keberuntungan

bandarcolok login

Statistik menunjukkan bahwa:

• Dalam jangka pendek, pemain bisa menang.

• Tapi dalam jangka panjang, hukum bilangan besar akan membuat hasil mendekati EV (yang biasanya negatif untuk pemain).

6. Sistem Martingale & Strategi Taruhan

Strategi seperti Martingale (melipatgandakan taruhan saat kalah) terlihat menarik, tapi:

• Tidak mengubah peluang dasar.

• Membutuhkan modal besar dan tidak memperhitungkan batas taruhan maksimum.

• Dalam jangka panjang tetap tunduk pada hukum statistik.

7. Kesimpulan

• Sistem taruhan dibangun untuk menguntungkan penyelenggara melalui keunggulan matematika.

• Memahami probabilitas dan expected value membantu pemain membuat keputusan lebih rasional.

• Tidak ada sistem taruhan yang bisa menjamin keuntungan dalam jangka panjang karena hukum probabilitas akan berlaku.